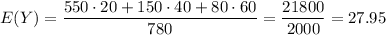Question

Russia has recently started a push for stronger smoking regulations much like those in Western countries concerning cigarette advertising, smoking in public places, and so on. The excel file named Russia contains sample data on smoking habits of Russians that are consistent with those reported by The Wall Street Journal (The Wall Street Journal, October 16, 2012). Analyze the data using Excel and answer the following questions. a. Develop a point estimate and a 95% confidence interval for the proportion of Russians who smoke. b. Develop a point estimate and a 95% confidence interval for the mean annual per capita consumption (number of cigarettes) of a Russian. c. For those Russians who do smoke, estimate the number of cigarettes smoked per day.

Answer 1

a) Point estimate p=0.39

The 95% confidence interval for the population proportion is (0.369, 0.411).

b) Point estimate M=10.9 cigarretes a day.

The 95% confidence interval for the mean is (10.84, 10.96).

c) 27.95 cigarretes per day.

Explanation:

The question is incomplete:

The sample data is not attached.

We can work with a random and representative sample where, from 2000 Russians interviewed, 780 are smokers.

Out of this 780 smokers, 550 smoke a package a day, 150 smoke two packages a day and 80 smoke three packages a day. The packages have 20 cigarettes each.

a) We have to calculate a 95% confidence interval for the proportion.

The score is X=780, with a sample size n=2000.

The point estimate for the sample population is the sample proportion and has a value of p=0.39.

`p=X/n=780/2000=0.39`

The standard error of the proportion is:

`\sigma_p=\sqrt{(p(1-p))/(n)}=\sqrt{(0.39*0.61)/(2000)}\\\\\\ \sigma_p=√(0.000119)=0.011`

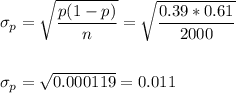
The critical z-value for a 95% confidence interval is z=1.96.

The margin of error (MOE) can be calculated as:

`MOE=z\cdot \sigma_p=1.96 \cdot 0.011=0.021`

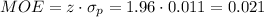
Then, the lower and upper bounds of the confidence interval are:

`LL=p-z \cdot \sigma_p = 0.39-0.021=0.369\\\\UL=p+z \cdot \sigma_p = 0.39+0.021=0.411`

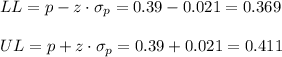
The 95% confidence interval for the population proportion is (0.369, 0.411).

b) The point estimate for the mean annual per capita consumption of cigarettes can be calculated as:

`M_X=(\sum n_iX_i)/(n)=(1220\cdot0+550\cdot 20+150\cdot 40+80\cdot 60)/(2000)\\\\\\M_X=(0+11000+6000+4800)/(2000)=(21800)/(2000)=10.9`

The standard deviation can be calculated as:

`s_X=\sqrt{(\sum n_i(X_i-M_x)^2)/(n-1)}\\\\\\s_X=\sqrt{(1220(0-10.9)^2+550(20-10.9)^2+150(40-10.9)^2+80(60-10.9)^2)/(1999)}\\\\\\s_X=\sqrt{(118.81+82.81+846.81+2410.81)/(1999)}=\sqrt{(3459.24)/(1999)}=√(1.73)\approx1.32`

We have to calculate a 95% confidence interval for the mean.

The population standard deviation is not known, so we have to estimate it from the sample standard deviation and use a t-students distribution to calculate the critical value.

The sample mean is M=10.9.

The sample size is N=2000.

When σ is not known, s divided by the square root of N is used as an estimate of σM:

`s_M=(s)/(√(N))=(1.32)/(√(2000))=(1.32)/(44.721)=0.03`

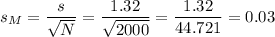
The degrees of freedom for this sample size are:

`df=n-1=2000-1=1999`

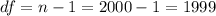
The t-value for a 95% confidence interval and 1999 degrees of freedom is t=1.961.

The margin of error (MOE) can be calculated as:

`MOE=t\cdot s_M=1.961 \cdot 0.03=0.06`

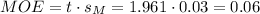
Then, the lower and upper bounds of the confidence interval are:

`LL=M-t \cdot s_M = 10.9-0.06=10.84\\\\UL=M+t \cdot s_M = 10.9+0.06=10.96`

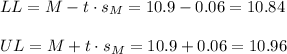
The 95% confidence interval for the mean is (10.84, 10.96).

c. Only for the proportion of smokers, the expected value for the number of cigarretes smoked per day is:

`E(Y)=(550\cdot 20+150\cdot 40+80\cdot 60)/(780)=(21800)/(2000)=27.95`