Question

When a hydrometer (see Fig. 2) having a stem diameter of 0.30 in. is placed in water, the stem protrudes 3.15 in. above the water surface. If the water is replaced with a liquid having a specific gravity of 1.10, how much of the stem would protrude above the liquid surface

Answer 1

5.79 in

Step-by-step explanation:

We are given that

Diameter,d=0.30 in

Radius,r=
`(d)/(2)=(0.30)/(2)=0.15 in`

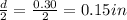
Weight of hydrometer,W=0.042 lb

Specific gravity(SG)=1.10

Height of stem from the water surface=3.15 in

Density of water=
`62.4lb/ft^3`

In water

Volume of water displaced
`V=(mass)/(density)=(0.042)/(62.4)=6.73* 10^(-4) ft^3`

Volume of another liquid displaced=
`V'=(V)/(SG)=(6.73* 10^(-4))/(1.19)=5.66* 10^(-4)ft^3`

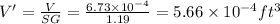
Change in volume=V-V'

`V-V'=\pi r^2 l`

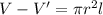
Substitute the values

`6.73* 10^(-4)-5.66* 10^(-4)=3.14* ((0.15)/(12))^2l`

By using

1 ft=12 in

`\pi=3.14`

`l=(6.73* 10^(-4)-5.66* 10^(-4))/(3.14* ((0.15)/(12))^2)`

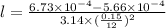
l=2.64 in

Total height=h+l=3.15+2.64= 5.79 in

Hence, the height of the stem protrude above the liquid surface=5.79 in