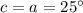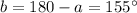Question

The sum of the measures of two of the angles formed by the intersection of two lines is 50°. Find the measures of the angles. I need four numbers, as in four angles

Answer 1

25°, 25°, 155° and 155°

Explanation:

Let's call the four angles a, b, c and d.

These angles are supplementary and vertically opposite in pairs, so we have:

`a = c`

`b = d`

`a + b = 180\°`

`c + d = 180\°`

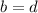
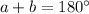
If the sum of two of these angles is 50°, these angles need to be the vertically opposite ones (a and c or b and d). So we have that:

`a + c = 50\°`

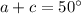
Substituting 'c' for 'a', we have:

`2a = 50`

`a = 25\°`

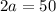
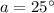
Now we can find the value of the three other angles:

`c = a = 25\°`

`b = 180 - a = 155\°`

`d = 180 - c = 155\°`