Answer:
The probability that the animal chosen is brown-haired is 0.6333.
Explanation:
Denote the events as follows:
A : a brown-haired rodent
B : Litter 1
The information provided is:
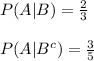
The probability of selecting any of the two litters is equal, i.e.
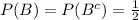
According to the law of total probability:
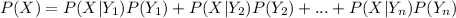
Compute the total probability of event A as follows:
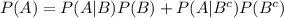
![=[(2)/(3)*(1)/(2)]+[(3)/(5)*(1)/(2)]\\\\=(1)/(3)+(3)/(10)\\\\=(10+9)/(30)\\\\=(19)/(30)\\\\=0.6333](https://img.qammunity.org/2021/formulas/mathematics/college/k286mmy23fispekqfqdcw0tejbrbkm1qao.png)
Thus, the probability that the animal chosen is brown-haired is 0.6333.