Question

Find f(x) + g(x), f(x) − g(x), f(x) · g(x), and f(x)/g(x). f(x) = x2 + 13x + 42 g(x) = x + 6 (a) f(x) + g(x) (b) f(x) − g(x) (c) f(x) · g(x) (d) f(x)/g(x)

Answer 1

(a) The value of f (x) + g (x) is
`x^(2)+4x+48`.

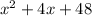(b) The value of f (x) - g (x) is
`x^(2) +12x+36`.

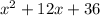(c) The value of f (x) · g (x) is
`x^(3)+19x^(2)+120x+252`.

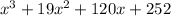(d) The value of f (x)/g (x) is
`(x+6)`.

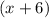Explanation:

The two polynomials provided are:

`f(x)=x^(2) + 13x + 42\\\\g(x)=x+6`

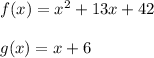
(a)

Compute the value of f (x) + g (x) as follows:

`f(x)+g(x)=(x^(2) + 13x + 42)+(x+6)`

`=x^(2) + 13x + 42+x+6\\\\=x^(2) + (13x+x)+(42+6)\\\\=x^(2) +14x+48`

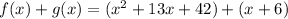
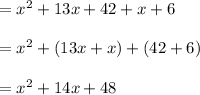
Thus, the value of f (x) + g (x) is
`x^(2)+4x+48`.

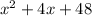(b)

Compute the value of f (x) - g (x) as follows:

`f(x)-g(x)=(x^(2) + 13x + 42)-(x+6)`

`=x^(2) + 13x + 42-x-6\\\\=x^(2) + (13x-x)+(42-6)\\\\=x^(2) +12x+36`

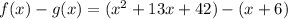
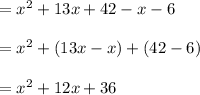
Thus, the value of f (x) - g (x) is
`x^(2) +12x+36`.

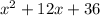(c)

Compute the value of f (x) · g (x) as follows:

`f(x)\cdot\ g(x)=(x^(2) + 13x + 42)\cdot(x+6)`

`=x^(2)\cdot(x+6)+13x\cdot(x+6)+42\cdot(x+6)\\\\=x^(3)+6x^(2)+13x^(2)+78x+42x+252\\\\=x^(3)+(6x^(2)+13x^(2))+(78x+42x)+252\\\\=x^(3)+19x^(2)+120x+252`

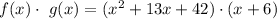
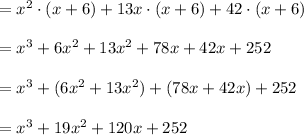
Thus, the value of f (x) · g (x) is
`x^(3)+19x^(2)+120x+252`.

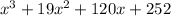(d)

Compute the value of f (x)/g (x) as follows:

`f(x)/ g(x)=((x^(2) + 13x + 42))/((x+6))`

`=((x^(2) + 7x + 6x + 42))/((x+6))\\\\=(x(x+7)+6(x+7))/((x+6))\\\\=((x+6)(x+7))/((x+6))\\\\=(x+6)`

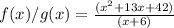
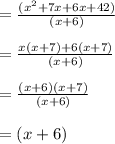
Thus, the value of f (x)/g (x) is
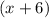`(x+6)`.