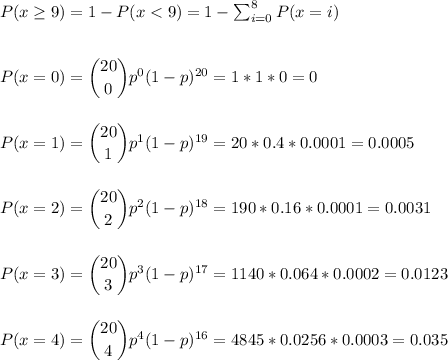Answer:
The probability that X is nine or more is 0.405.
Explanation:
We have a sample of 20 random selected workers, each with a probability p=0.4 of changing jobs for "slightly higher pay".
We have a random variable X that can be modeled by the binomial distribution, with parameters n=20 (sample size) and p=0.4 (probability of success).
The probability that k workers will change jobs for slightly higher pay can be calcualted as:
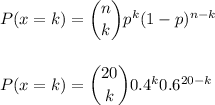
We have to calculate the probability that the number of workers in the sample who will change jobs for slightly higher pay is 9 or higher. That is P(X≥9).