Question

The percent defective for parts produced by a manufacturing process is targeted at 4%. The process is monitored daily by taking samples of sizes n = 160 units. Suppose that today’s sample contains 14 defectives. How many units would have to be sampled to be 95% confident that you can estimate the fraction of defective parts within 2% (using the information from today’s sample--that is using the result that f$hat {767} =0.0875f$

Answer 1

`n=(0.0875(1-0.0875))/(((0.02)/(1.96))^2)=766.82`

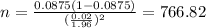
And rounded up we have that n=767

Explanation:

We know the following info:

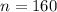`n=160` represent the sample size selected

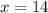`x= 14` represent the number of defectives in the sample

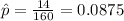`\hat p= (14)/(160)= 0.0875` represent the estimated proportion of defectives

`ME = 0.02` represent the margin of error desired

The margin of error for the proportion interval is given by this formula:

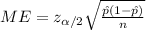`ME=z_(\alpha/2)\sqrt{(\hat p (1-\hat p))/(n)}` (a)

And on this case we have that
`ME =\pm 0.02` and we are interested in order to find the value of n, if we solve n from equation (a) we got:

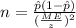`n=(\hat p (1-\hat p))/(((ME)/(z))^2)` (b)

The crtical value for a confidence level of 95% is
`z_(\alpha/2)=1.96`

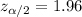
And replacing into equation (b) the values from part a we got:

`n=(0.0875(1-0.0875))/(((0.02)/(1.96))^2)=766.82`

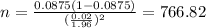
And rounded up we have that n=767