Question

To illustrate the law of large numbers (see also Exercise 5.54 on page 172), use the normal approximation to the binomial distribution to determine the probabilities that the proportion of heads will be anywhere from 0.49 to 0.51 when a balanced coin is flipped

(a) 100 times;

(b) 1,000 times;

(c) 10,000 times.

Answer 1

(a) 0.1585

(b) 0.4713

(c) 0.9545

Step-by-step explanation:

The random variable X can be defined as the number of heads.

The coin provided is balanced, i.e. P (H) = P (T) = 0.50

The outcome of tossing the coin are: (H and T). Each of these outcomes are independent of each other.

The random variable X thus follows a Binomial distribution with probability of success as 0.50.

For a large sample a Normal approximation to binomial can be applied to approximate the distribution of p if the following conditions are satisfied:

1. np ≥ 10

2. n(1 - p) ≥ 10

(a)

n = 100

Check the conditions as follows:

`np=100* 0.50=50>10\\\\n(1-p)=100*(1-0.50)=50>10`

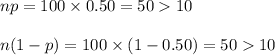
Thus, a Normal approximation to binomial can be applied.

So,
`p\sim N(0.50,\ 0.05 )`

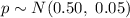
Compute the probability hat the proportion of heads will be anywhere from 0.49 to 0.51 as follows:

`P(0.49<p<0.51)=P((0.49-0.50)/(0.05)<(p-\mu)/(\sigma)<(0.51-0.50)/(0.05))`

`=P(-0.20<Z<0.20)\\\\=P(Z<0.20)-P(Z<-0.20)\\\\=0.57926-0.42074\\\\=0.15852\\\\\approx 0.1585`

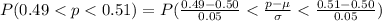
Thus, the probability hat the proportion of heads will be anywhere from 0.49 to 0.51 when a balanced coin is flipped 100 times is 0.1585.

(b)

n = 1000

Check the conditions as follows:

`np=1000* 0.50=500>10\\\\n(1-p)=1000*(1-0.50)=500>10`

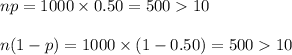
Thus, a Normal approximation to binomial can be applied.

So,
`p\sim N(0.50,\ 0.016 )`

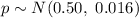
Compute the probability hat the proportion of heads will be anywhere from 0.49 to 0.51 as follows:

`P(0.49<p<0.51)=P((0.49-0.50)/(0.016)<(p-\mu)/(\sigma)<(0.51-0.50)/(0.016))`

`=P(-0.63<Z<0.63)\\\\=P(Z<0.63)-P(Z<-0.63)\\\\=0.73565-0.26435\\\\=0.4713`

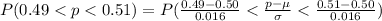
Thus, the probability hat the proportion of heads will be anywhere from 0.49 to 0.51 when a balanced coin is flipped 1000 times is 0.4713.

(c)

n = 10,000

Check the conditions as follows:

`np=10000* 0.50=5000>10\\\\n(1-p)=10000*(1-0.50)=5000>10`

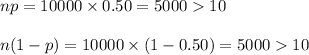
Thus, a Normal approximation to binomial can be applied.

So,
`p\sim N(0.50,\ 0.005)`

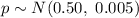
Compute the probability hat the proportion of heads will be anywhere from 0.49 to 0.51 as follows:

`P(0.49<p<0.51)=P((0.49-0.50)/(0.005)<(p-\mu)/(\sigma)<(0.51-0.50)/(0.005))`

`=P(-2<Z<2)\\\\=P(Z<2)-P(Z<-2)\\\\=0.97725-0.02275\\\\=0.9545`

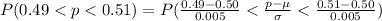
Thus, the probability hat the proportion of heads will be anywhere from 0.49 to 0.51 when a balanced coin is flipped 10,000 times is 0.9545.