Answer:
Option A
Explanation:
We are given that
Scale factor=2
Center of dilation=(0,0)
Point A(0,2) and point B (2,0).
Slope of line f=
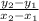
Substitute the values
Slope of line f=
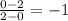
Distance between A and Origin (0,0) is given by
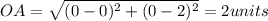
Using distance formula
OB=
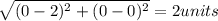
Length of OA'=2OA=2(2)=4 units
Length of OB'=2(OB)=2(2)=4 units
x-intercept of line f' at x=4
y-intercept of line f' at y=4
Therefore, the points A' and B' are given by
(0,4) and (4,0)
Slope of line f'=
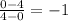
Slope of line f and f' are equal.Therefore, lines f and f' are parallel.
Option A is true.