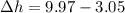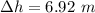Question

A place-kicker must kick a football from a point 36.0 m (about 40 yards) from the goal. Half the crowd hopes the ball will clear the crossbar, which is 3.05 m high. When kicked, the ball leaves the ground with a speed of 21.6 m/s at an angle of 50.0° to the horizontal.

Required:
By how much does the ball clear or fall short (vertically) of clearing the crossbar?

Answer 1

The difference is height is
`\Delta h =6.92 \ m`

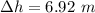
Step-by-step explanation:

From the question we are told that

The distance of ball from the goal is
`d = 36.0 \ m`

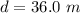
The height of the crossbar is
`h = 3.05 \ m`

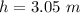
The speed of the ball is
`v = 21.6 \ m/s`

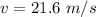
The angle at which the ball was kicked is
`\theta = 50 ^o`

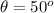
The height attained by the ball is mathematically represented as

`H = v_v * t - (1)/(2) gt^2`

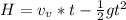
Where
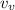`v_v` is the vertical component of velocity which is mathematically represented as

`v_v = v * sin (\theta )`

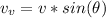
substituting values

`v_v = 21.6 * (sin (50 ))`

`v_v = 16.55 \ m/s`

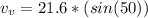
Now the time taken is evaluated as

`t = (d)/(v * cos(\theta ))`

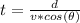
substituting value

`t = (36)/(21.6 * cos(50 ))`

`t = 2.593 \ s`

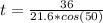
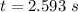
So

`H = 16.55 * 2.593 - (1)/(2) * 9.8 * (2.593)^3`

`H = 9.97 \ m`

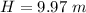
The difference in height is mathematically evaluated as

`\Delta h = H - h`

substituting value

`\Delta h = 9.97 - 3.05`

`\Delta h =6.92 \ m`