Answer:
a. F = 2.32*10^-18 N
b. The force F is 2.59*10^11 times the weight of the electron
Step-by-step explanation:
a. In order to calculate the magnitude of the force exerted on the electron you first calculate the acceleration of the electron, by using the following formula:
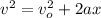 (1)
(1)
v: final speed of the electron = 6.60*10^5 m/s
vo: initial speed of the electron = 4.00*10^5 m/s
a: acceleration of the electron = ?
x: distance traveled by the electron = 5.40cm = 0.054m
you solve the equation (2) for a and replace the values of the parameters:
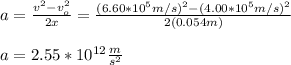
Next, you use the second Newton law to calculate the force:
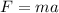
m: mass of the electron = 9.11*10^-31kg
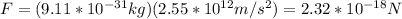
The magnitude of the force exerted on the electron is 2.32*10^-18 N
b. The weight of the electron is given by:
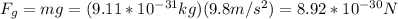
The quotient between the weight of the electron and the force F is:

The force F is 2.59*10^11 times the weight of the electron