Question

The table represents an exponential function.

What is the multiplicative rate of change of the function?
3
WINX
19 2
y
6
4
8
3
16
9
2
9
4

Answer 1

b=2/3

Explanation:

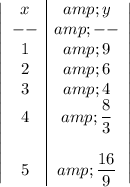
The table is given as:

`\left|\begin{array}cx&y\\--&--\\1&9\\2&6\\3&4\\4&\frac83\\\\5&(16)/(9)\end{array}\right|`

The exponential function is given in the form

`y= a (b)^(x)`

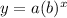
where a is the initial value and b is the multiplicative rate of change

When x=1, y=9, we have:

`9= a (b)^(1)`

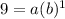
When x=3, y=4, we have:

`4= a (b)^(3)`

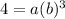
Dividing the two equations:

`(a (b)^(3))/(a (b)^(1)) =(4)/(9) \\b^2=(4)/(9)\\b=\sqrt{(4)/(9)} \\b=(2)/(3)`

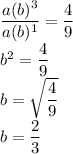
The multiplicative rate of change, b is 2/3.