Question

Find the regression​ equation, letting the first variable be the predictor​ (x) variable. Using the listed​ lemon/crash data, where lemon imports are in metric tons and the fatality rates are per​ 100,000 people, find the best predicted crash fatality rate for a year in which there are 525 metric tons of lemon imports. Is the prediction​ worthwhile?

Lemon Imports 226264-366-470-539-



Crash Fatality Rate 16 157 15.4 15.3 15

Answer 1

The equation of regression is

`y = 16.522 - 0.00279 \cdot x`

The predicted crash fatality rate is 15.057 for 525 metric tons of lemon import.

Explanation:

We are given the following lemon/crash data,

Lemon Imports = 226 264 366 470 539

Crash Fatality Rate = 16 15.7 15.4 15.3 15

The regression​ equation is given by

`y = a + b \cdot x`

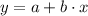
where x is the lemon imports in metric tons and y is the fatality rate per​ 100,000 people.

The constants b is the slope and a is the y-intercept of the regression line and are given by

`$ a = (\sum Y * \sum X^2 - \sum X * \sum XY )/(n * \sum X^2 - (\sum X)^2) $`

`$ b = (n * \sum XY - \sum X * \sum Y )/(n * \sum X^2 - (\sum X)^2) $`

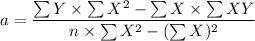
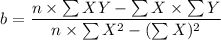
Using Excel to find
`\sum X, \sum Y, \sum XY, \sum X^2`

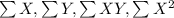
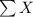`\sum X` = 1865

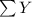`\sum Y` = 77.4

`\sum XY` = 28673.2

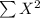`\sum X^2` = 766149

So the constants a and b are

`$ a = (77.4 * 766149 - 1865 * 28673.2 )/(5 * 766149 - (1865)^2) $`

`a = 16.522`

`$ b = (5 * 28673.2 - 1865 * 77.4 )/(5 * 766149 - (1865)^2) $`

`b = -0.00279`

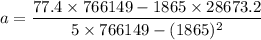
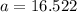
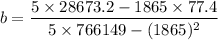
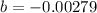
Therefore, the equation of regression is

`y = a + b \cdot x \\\\y = 16.522 - 0.00279 \cdot x`

The best predicted crash fatality rate for a year in which there are 525 metric tons of lemon imports is given by

`y = 16.522 - 0.00279 \cdot (525) \\\\y = 16.522 - 1.465 \\\\y = 15.057`

The predicted crash fatality rate of 15.057 for 525 metric tons of lemon import seems to be satisfactory since it lies between the crash fatality rate of 15 to 15.3 for lemon imports of 539 to 470.