Question

Assume that you plan to use a significance level of α = 0.05 to test the claim that p1 = p2. Use the given sample sizes and numbers of successes to find the pooled estimate. Round your answer to the nearest thousandth.

n1 = 677 n2 = 3377
x1 = 172 x2 = 654

Answer 1

The calculated value Z = 3.775 > 1.96 at 0.05 level of significance

Null hypothesis is rejected

The Two Population proportion are not equal

Explanation:

Given first sample size n₁ = 677

First sample proportion

`p^(-) _(1) = (x_(1) )/(n_(1) ) = (172)/(677) = 0.254`

Given second sample size n₂ = 3377

second sample proportion

`p^(-) _(2) = (x_(2) )/(n_(2) ) = (654)/(3377) = 0.1936`

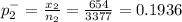
Null Hypothesis : H₀ : p₁ = p₂.

Alternative Hypothesis : H₁ : p₁ ≠ p₂.

Test statistic

`Z = \frac{p_(1) ^(-)-p^(-) _(2) }{\sqrt{P Q((1)/(n_(1) ) +(1)/(n_(2) )) } }`

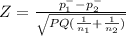
where

`P = (n_(1) p_(1) + n_(2) p_(2) )/(n_(1)+n_(2) ) = (677 X 0.254+3377 X 0.1936)/(677+3377)`

P = 0.2036

Q = 1 - P = 1 - 0.2036 = 0.7964

`Z = \frac{0.254- 0.1936 }{\sqrt{0.2036 X 0.7964((1)/(677 ) +(1)/(3377 )) } }`

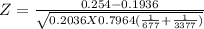
Z = 3.775

Critical value ∝=0.05

Z- value = 1.96

The calculated value Z = 3.775 > 1.96 at 0.05 level of significance

Null hypothesis is rejected

The Two Population proportion are not equal