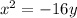Question

Find the standard form of the equation of the parabola with a vertex at the origin and a focus at (0.-4).

Oy=-x?
Oy2 = -4x
Oy2 = -16%
Oyə tox?

Answer 1

`x^2 = -16y`

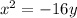
Explanation:

Given

`Vertex = (0,0)\\Focus = (0,-4)`

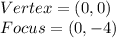
Required

Equation of the parabola (in standard form)

The standard form of a parabola is
`(x - h)^2 = 4p (y - k),`

Such that

Vertex = (h,k)

Focus = (h, k + p)

For the vertex

This implies that (h,k) = (0,0)

h = 0 and k = 0

For the focus

This implies that (h, k + p) = (0, -4)

`h = 0\\k + p = -4`

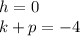
Recall that
`k = 0;`

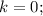
Hence,
`0 + p = -4`

`p = -4`

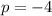
Substitute
`p = -4`,
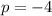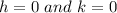`h = 0\ and\ k = 0` in the given formula

`(x - h)^2 = 4p (y - k),` becomes

`(x - 0)^2 = 4 * -4 (y - 0),`

`(x)^2 = 4 * -4 (y),`

`x^2 = -16 (y),`

`x^2 = -16y`

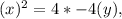
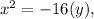
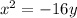
Hence,, the standard form is
`x^2 = -16y`