Answer:
Explanation:
We have 3 triangles here, all of them right triangles. The first one is the biggest one, triangle ABC. We know the side length AB = 14, and we know the hypotenuse length, BC = 30. We can use that, along with Pythagorean's Theorem, to solve for side length AC:
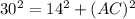 and
and
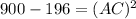 and
and
 so
so
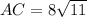
We also have the smallest right triangle, triangle ABD, which has the base of x, our unknown. Side BD is our unknown, length x; side AD is the height, length y (also unknown); and side AB is the hypotenuse, length 14. We will come up with a system of equations for these 2 right triangles, using Pythagorean's Theorem, and then solve for x using substitution.
For the medium-sized triangle. triangle ADC, the hypotenuse is side AC with a measure of 8√11, the height is side AD length y, and the base is side DC length 30 - x. Putting those values into Pythagorean's Theorem:
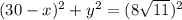 and
and
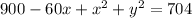 and
and
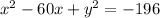 *** That's starred because it's important and we will come back to it.
*** That's starred because it's important and we will come back to it.
The smallest triangle in Pythagorean's Theorem:
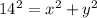 and solving that for y-squared:
and solving that for y-squared:
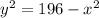 . We will now sub that value for y-squared into the starred equation for y-squared and solve for x:
. We will now sub that value for y-squared into the starred equation for y-squared and solve for x:
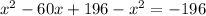 and
and
-60x = -392 so
x = 6.5