Question

A cylinder has a base diameter of 5 cm and a height of 8 cm.

The base diameter is increased by 15% and the height is decreased by 30%.
Find the percentage change in the volume of the cylinder.
Type each step of your working on a separate line.

Answer 1

The new volume is 81.2% of the prior, this is true for any for any values of radius and height, as long as they are changed as stated.

Explanation:

The volume of a cylinder is given by:

`V = \pi*r^2*h`

If we increase the diameter by 15%, then the radius is increased by 7.5% and the new radius is:

`r_(new) = 1.075*r`

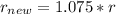
If we decrease the height by 30%, then the new height is 70% of the prior and is given by:

`h_(new) = 0.7*h`

Applying to the volume formula we have:

`V_(new) = pi*(r_(new))^2*h_(new)`

`V_(new) = \pi*(1.075*r)^2*0.7*h\\V_(new) = 1.16*0.7*\pi*r^2*h\\V_(new) = 0.812*\pi*r^2*h\\V_(new) = 0.812*V`

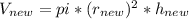
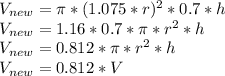
The new volume is 81.2% of the prior, this is true for any for any values of radius and height, as long as they are changed as stated.