Answer:
a) 8.33 x
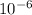 Pa or 8.22 x
Pa or 8.22 x
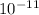 atm
atm
b) 1.66 x
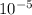 Pa or 1.63 x
Pa or 1.63 x
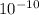 atm
atm
c) 2.77 x
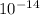 kg/m^2-s
kg/m^2-s
Step-by-step explanation:
Intensity of light = 2500 W/m^2
area = 25 ft^2
a) average radiation pressure on a totally absorbing section of the floor
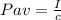
where I is the intensity of the light
c is the speed of light =
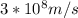
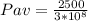 = 8.33 x
= 8.33 x
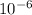 Pa
Pa
1 pa =

8.33 x
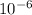 Pa = 8.22 x
Pa = 8.22 x
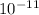 atm
atm
b) average radiation for a totally radiating section of the floor
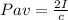
this means that the pressure for a totally radiating section is twice the average pressure of the totally absorbing section
therefore,
Pav = 2 x 8.33 x
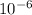 = 1.66 x
= 1.66 x
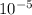 Pa
Pa
or
Pav in atm = 2 x 8.22 x
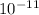 = 1.63 x
= 1.63 x
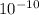 atm
atm
c) average momentum per unit volume is
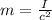
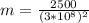 = 2.77 x
= 2.77 x
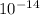 kg/m^2-s
kg/m^2-s