Answer:
40 ft
Explanation:
Triangle ABC is given by AB = 13 ft, BC = 10 ft, ∠ACB = 50° and AC = b. Let AB = a = 13 ft, BC = c = 10 ft
Since two sides are given and one angle is given, to find the other side, we use the cosine formula. The cosine formula is given by:
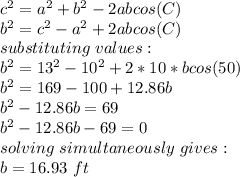
The perimeter of the triangle is given by:
Perimeter = AB + BC + AC = 13 + 10 +16.93 = 39.93 ft ≈ 40 ft