Question

A compact disc rotates from rest up to an angular speed of 31.4 rad/s in a time of 0.892 s.

(a) What is the angular acceleration of the disc, assuming the angular acceleration is uniform?
(b) Through what angle does the disc turn while coming up to speed?
(c) If the radius of the disc is 4.45 cm, find the tangential speed of a microbe riding on the rim of the disc when t=0.892 s.
(d) What is the magnitude of the tangential acceleration at the given time?

Answer 1

(a) α = 35.20 rad/s^2

(b) θ = 802°

(c) v = 139.73 cm/s

(d) a = 156.64 cm/s^2

Step-by-step explanation:

(a) To find the angular acceleration of the disc you use the following formula:

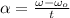`\alpha=(\omega-\omega_o)/(t)` (1)

w: angular speed of the disc = 31.4 rad/s

wo: initial angular speed = 0 rad/s

t: time = 0.892s

You replace the values of the parameters in the equation (1):

`\alpha=(31.4rad/s-0rad/s)/(0.892s)=35.20(rad)/(s^2)`

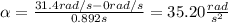
The angular acceleration of the disc, for the given time, is 35.20rad/s^2

(b) To calculate the angle describe by the disc in such a time you use:

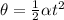`\theta=(1)/(2)\alpha t^2` (2)

`\theta=(1)/(2)(35.20rad/s^2)(0.892s)^2=14.00rad`

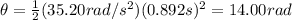
In degrees you have:

`\theta=14.00rad*(180\°)/(\pi \ rad)=802\°`

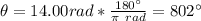
The angle described by the disc is 802°

(c) To calculate the tangential speed of the microbe for t=0.892s, you use the following formula:

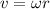`v=\omega r` (3)

w: angular speed for t = 0.892s = 31.4rad/s

r: radius of the disc = 4.45cm

`v=(31.4rad/s)(4.45cm)=139.73(cm)/(s)`

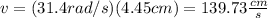
The tangential speed is 139.73 cm/s

(d) The tangential acceleration is calculated by using the following formula:

`a=\alpha r`

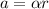
α: angular acceleration for t=0.892s

`a=(35.20rad/s^2)(4.45cm)=156.64(cm)/(s^2)`

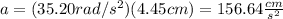
The tangential acceleration is 156.64cm/s^2