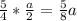Answer:
A)
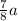
B)
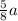
Explanation:
AB has length a and is divided by points P and Q into AP , PQ , and QB , such that AP = 2PQ = 2QB
A) Therefore, AP = 2QB
QB = AP/2
The midpoint of QB = QB/2 = (AP/2)/2 = AP/4
AP = 2PQ, Therefore PQ = AP/2
Since the length of AB = a
AB = AP + PQ + QB = a
AP + AP/2 + AP/2 = a
AP + AP = a
2AP = a
AP = a/2
The distance between point A and the midpoint of segment QB = AP + PQ + QB/2 = AP + AP/2 + AP/4 = 7/4(AP)
But AP = a/2
Therefore The distance between point A and the midpoint of segment QB = 7/4(a/2)=
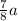
B)
the distance between the midpoints of segments AP and QB = AP/2 + PQ + QB/2 = AP/2 + AP/2 + AP/4 = 5/4(AP)
But AP = a/2
Therefore the distance between the midpoints of segments AP and QB = 5/4(AP) =