Answer:
x=27
Explanation:
To evaluate the expression:
![[(3^(-5))(3^4)]^3](https://img.qammunity.org/2021/formulas/mathematics/high-school/7y427zxvagx10ufbcypsny15yj1osja7am.png)
Step 1: Innermost group, apply the product of powers (
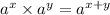
Therefore:
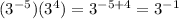
We then have:
![=[3^(-1)]^3](https://img.qammunity.org/2021/formulas/mathematics/high-school/p670xkh357v3npy55tstnkqq9hwkfj2efr.png)
Step 2: Apply the power of a power
![[3^(-1)]^3=3^(-1 * 3) =3 ^(-3)](https://img.qammunity.org/2021/formulas/mathematics/high-school/ncpv6qb4lgkvnm1a1oo99ns27p4gq9tsof.png)
Step 3: Apply the negative exponent
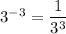
Step 4: Simplify
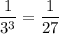
Therefore, the value of x in the simplified expression is 27.