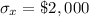Answer:
1.
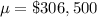
2.

3.
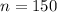
4.
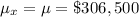
5.
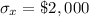
Explanation:
The average mortgage owed by Americans is $306,500, with a standard deviation of $24,500.
From the above information, we know that,
The population mean is
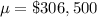
The population standard deviation is

Suppose a random sample of 150 Americans is selected
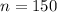
Since the sample size is quite large then according to the central limit theorem, the sample mean is approximately normally distributed.
The sample mean would be the same as the population mean that is
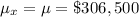
The sample standard deviation is given by
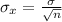
Where
 is the population standard deviation and n is the sample size.
is the population standard deviation and n is the sample size.

Therefore, the required parameters are:
1.
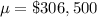
2.

3.
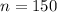
4.
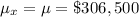
5.