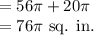Question

A firework rocket consists of a cone stacked on top of a cylinder, where the radii of the cone and the cylinder are equal. The diameter of the cylindrical base of the rocket is 8 in and the height of the cylinder is 5 in, while the height of the cone is 3 in. Calculate the surface area of the rocket. Leave your answer in terms of π. 184π sq. in. 76π sq. in. 168π sq. in. 88π sq. in.

Answer 1

The answer is 76π sq. in.

Explanation:

Took the quiz and that was correct.

Answer 2

(B)
`76\pi$ sq. in.`

Explanation:

Since the base of the cone and one circular face of the cylinder is not visible,

The surface area of the rocket=Base Area of the Cylinder+Lateral area of the Cylinder+Lateral Area of the Cone+

`R$adius =4 Inches\\Height of the cylinder =5 Inches\\Therefore:\text{Lateral area of a Cylinder+Base Area of the Cylinder}=2\pi rh+\pi r^2\\=(2* \pi * 4 * 5)+(\pi * 4^2)\\=40\pi+16\pi \\=56\pi$ sq. in.`

Lateral Area of a Cone
`=\pi rl`

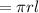
• Base radius, r= 8/2 =4 Inches
• Perpendicular Height of the Cone = 3 Inches

Using Pythagoras theorem:

`Hypotenuse =√(opposite^2+adjacent^2) \\=√(3^2+4^2) \\=√(25)\\ =5 in.`

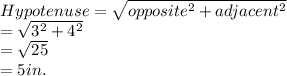
• Slant Height of the Cone, l (Hypotenuse) = 5 Inches

Therefore: Lateral Area of a Cone
`=\pi * 4* 5 =20\pi$ sq. in.`

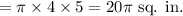
Therefore, Surface area of the rocket

`=56\pi+20\pi\\=76\pi$ sq. in.`