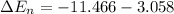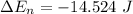Question

A 0.26-kg stone is held 1.2 m above the top edge of a water well and then dropped into it. The well has a depth of 4.5 m. (a) Relative to the configuration with the stone at the top edge of the well, what is the gravitational potential energy of the stone−Earth system before the stone is released?

Answer 1

Complete Question

The

Answer:

a

`E_r = 3.058 \ J`

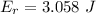
b

`E_b = -11.466 \ J`

c

`\Delta E_n = -14.524 \ J`

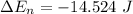
Step-by-step explanation:

From the question we are told that

The mass of the stone is
`m_s = 0.26 \ kg`

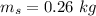
The height above the top of the water is
`h = 1.2 \ m`

The depth of the well is
`d = 4.5 \ m`

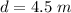
The gravitational potential of the stone before it was released is

`E_r = mgh`

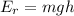
substituting values

`E_r = 0.26 * 9.8 * 1.2`

`E_r = 3.058 \ J`

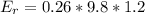
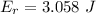
The gravitation potential of the stone when it reaches the bottom of the well is

`E_b = mg(- d)`

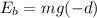
The negative shows that the potential energy of the stone as compared to the earth is reducing

substituting values

`E_b = 0.26 * 9.8 *(- 4.5)`

`E_b = -11.466 \ J`

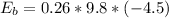
The change in the systems gravitational potential is

`\Delta E_n = E_b - E_r`

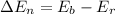
substituting values

`\Delta E_n = -11.466 - 3.058`

`\Delta E_n = -14.524 \ J`