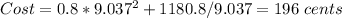Answer:
base side = 9.037 inches
height = 6.024 inches
Minimum cost = 196 cents
Explanation:
The volume of the bin is given by:
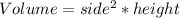
and the surface area of the bin is given by:
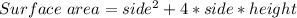
The cost of the bin will be:
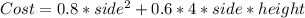
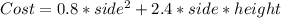
From the volume equation, we have:
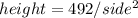
Now the cost will be:
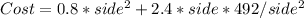
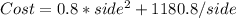
To find the side that gives the minimum cost, we can find the derivative of Cost in relation to side and then make it equal zero:
Abbreviating Cost as C and side as s, we have:
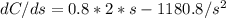
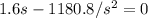
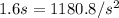
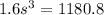
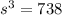
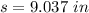
Finding the height of the bin, we have:
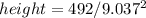
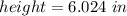
The minimum cost is: