Answer:
The dilation is twice the original form
Explanation:
Given
Original Triangle = ABC
Dilated Image = A'B'C'
Required
Relationship between both
From the attached diagram;

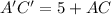
This implies that
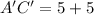

The relationship between a dilated image and its original form is;
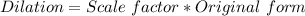
Using AC and A'C';
Such that A'C" is the Dilation image of AC
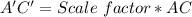
Replace AC an A'C' with their lengths
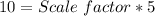
Divide both sides by 5
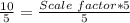
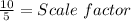
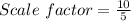
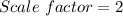
Hence, the dilation is twice the original form