Answer:
The UCL is 3.636 and the LCL is 2.964.
Explanation:
The complete question is:
Construct a control chart for the Lard-O example using 3 sigma limits if samples of size 10 are randomly selected from the process. The center line is 3.3. The standard deviation of the sample mean is 0.112. The UCL = ____. The LCL = ____.
Solution:
The control chart is a graphical display used to study how a process changes over time. The data are plotted in time order.
The parts of a control chart are a central line for the average, an upper line for the upper control limit, and a lower line for the lower control limit.
These lines are formed using the historical data.
The information provided is:
Center line = m = 3.3
Standard deviation = s = 0.112
Compute the 3σ upper control limit as follows:
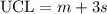

Compute the 3σ lower control limit as follows:
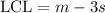
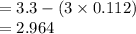
Thus, the UCL is 3.636 and the LCL is 2.964.