Question

14. Suppose that 1 out of every 10,000 doctors in a certain region is infected with the SARS virus; in the same region, 20 out of every 100 people in a particular at-risk population also are infected with the virus. A test for the virus gives a positive result in 99% of those who are infected and in 1% of those who are not infected. A randomly selected doctor and a randomly selected person in the at-risk population in this region both test positive for the disease. Who is more likely to actually have the disease?

Answer 1

The person in the at-risk population is much more likely to actually have the disease

Explanation:

The probability of a randomly selected doctor having the disease is 1 in 1,000 (P(I)=0.0001).

The probability that a doctor is infected with SARS, given that they tested positive is:

`P(I|+)=(P(I)*0.99)/(P(I)*0.99+(1-P(I))*0.01)\\P(I|+)=(0.0001*0.99)/(0.0001*0.99+(1-0.0001)*0.01)\\P(I|+)=9.9*10^(-3)`

The probability of a randomly selected person from the at-risk population having the disease is 20 in 100 (P(I)=0.20).

The probability that a person in the at-risk population is infected with SARS, given that they tested positive is:

`P(I|+)=(P(I)*0.99)/(P(I)*0.99+(1-P(I))*0.01)\\P(I|+)=(0.2*0.99)/(0.2*0.99+(1-0.2)*0.01)\\P(I|+)=0.962`

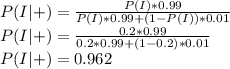
Therefore, the person in the at-risk population is much more likely to actually have the disease