Question

Let p, q be the solutions of the quadratic equation x^2 − 2mx − 5n = 0 and let m, n be the solutions of x^2 − 2px − 5q = 0. If p,q,m and n are real and non-equal, then the value of p + q + m + n is ....

(A) 15

(B) 30

(C) 75

(D) 150

(E) 225​

Answer 1

The correct option is;

(B) 30

Explanation:

The equations are;

x² - 2·m·x - 5·n = 0.............(1)

Solution = p, q

x² - 2·p·x - 5·q = 0..............(2)

Solution = m, n

For equation (1), we have;

x² - 2·m·x - 5·n = 0 = (x - p)·(x - q)

x² - 2·m·x - 5·n = x² -x·p - x·q + q·p = x² -x·(p + q) + q·p

2·m = p + q..............(3)

5·n = -q·p..............(4)

Given the similarity between equation (1) and (2), we have;

2·p = m + n..............(5)

5·q = -m·n..............(6)

Therefore;

m = (p + q)/2

n = -q·p/5

Substituting the value of m and n in equation (5) and (6), we have;

2·p = (p + q)/2 - q·p/5.............(7)

5·q = (p + q)/2·q·p/5.............(8)

Making q the subject of equation (7) gives;

`q = (-7.5 \cdot p)/(p -2.5)`

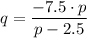
Substituting the value of q above in equation (8) gives;

`-(75\cdot p)/(2\cdot p-5)=-(3\cdot p^(4)-30\cdot p^(3))/(4\cdot p^(2)-20\cdot p+25)`

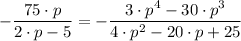
By cross multiplying and collecting like terms we have;

6·p⁵ -75·p⁴-150·p³+1500·p²-1875·p = 0

Which gives

(p+0)(p-1.91)(p-2.5)(p+5)(p-13.1)

p = 1.91 or 2.5 or -5 or 13.1

q = 24.27 or undef or -5 or -9.27

m = 13.09 or undef or -5 or 1.95

n = -9.27 or undef or -5 or -24.29

Therefore, p + q + m + n = 1.91 + 24.27 + 13.09 + (-9.27) = 30

The correct option is (B) 30