Question

|2x − 1| = |4x + 9| please solve these i want hurryly

Answer 1

`\boxed{\sf \ the \ solutions \ are \ -5 \ and \ -4/3 \ }`

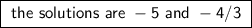
Explanation:

Hello,

we need to find x so that

|2x-1|=|4x+9|

and we know that |x|=x if x >= 0 -x otherwise

2x-1=0 <=> 2x=1 <=> x = 1/2

4x+9=0 <=> 4x=-9 <=> x = -9/4

So we need to work in three different intervals

case 1: x <= -9/4 ( <= 1/2)

so |2x-1| = -(2x-1) = -2x+1

and |4x+9| = -4x-9

so we need to solve -2x+1=-4x-9<=> 2x=-9-1=-10 <=> x = -5

case 2: -9/4 <= x <= 1/2

so |2x-1| = -(2x-1) = -2x+1

and |4x+9| = 4x+9

so we need to solve -2x+1=4x+9<=> 6x=1-9=-8 <=> x = -8/6 = -4/3

case 3: -9/4 <= 1/2 <= x

so |2x-1| = 2x-1

and |4x+9| = 4x+9

so we need to solve 2x-1=4x+9<=> 2x=-1-9=-10 <=> x = -10/2 = -5

Finally, the solutions are -5 and -4/3

to verify, you can see below the graph of the two functions