Question

What is the value of S, for ΣΒ(2) -
=1
Ο 43
84
90
ΘΕ

Answer 1

Option (3)

Explanation:

Given expression in this question represents the partial sum of an infinite geometric series in the sigma notation.

`S_(n)=\sum_(n=1)^(\infty)6(2)^(n-1)`

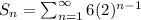
First term of this series 'a' = 6

Common ratio 'r' = 2

We have to find the sum of 4 terms of this infinite series (n = 4).

Sum of n terms of a geometric series is,

`S_n=(a(r^n-1))/((r-1))`

`S_4=(6(2^4-1))/((2-1))`

`=(6(16-1))/((1))`

`=90`

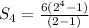
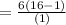
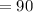
Therefore, sum of 4 terms of the given series will be 90.

Option (3) will be the answer.