Question

A 36.0 kg box initially at rest is pushed 5.00 m along a rough, horizontal floor with a constant applied horizontal force of 130 N. If the coefficient of friction between box and floor is 0.300, find the following.

(a) the work done by the applied force,
(b) the increase in internal energy in the box–floor system as a result of friction,
(c) the work done by the normal force,
(d) the work done by the gravitational force,
(e) the change in kinetic energy of the box, and
(f) the final speed of the box.

Answer 1

(a) W = 650J

(b) Wf = 529.2J

(c) W = 0J

(d) W = 0J

(e) ΔK = 120.8J

(f) v2 = 2.58 m/s

Step-by-step explanation:

(a) In order to find the work done by the applied force you use the following formula:

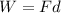`W=Fd` (1)

F: applied force = 130N

d: distance = 5.0m

`W=(130N)(5.0m)=650J`

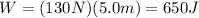
The work done by the applied force is 650J

(b) The increase in the internal energy of the box-floor system is given by the work done of the friction force, which is calculated as follow:

`W_f=F_fd=\mu Mgd` (2)

μ: coefficient of friction = 0.300

M: mass of the box = 36.0kg

g: gravitational constant = 9.8 m/s^2

`W_f=(0.300)(36.0kg)(9.8m/s^2)(5.0m)=529.2J`

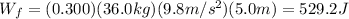
The increase in the internal energy is 529.2J

(c) The normal force does not make work on the box because the normal force is perpendicular to the motion of the box.

`W = 0J`

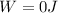
(d) The same for the work done by the normal force. The work done by the gravitational force is zero because the motion of the box is perpendicular o the direction of the gravitational force.

(e) The change in the kinetic energy is given by the net work on the box. You use the following formula:

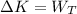`\Delta K=W_T` (3)

You calculate the total work:

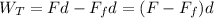`W_T=Fd-F_fd=(F-F_f)d` (4)

F: applied force = 130N

Ff: friction force

d: distance = 5.00m

The friction force is:

`F_f=(0.300)(36.0kg)(9.8m/s^2)=105.84N`

Next, you replace the values of all parameters in the equation (4):

`W_T=(130N-105.84N)(5.00m)=120.80J`

`\Delta K=120.80J`

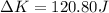
The change in the kinetic energy of the box is 120.8J

(e) The final speed of the box is calculated by using the equation (3):

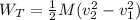`W_T=(1)/(2)M(v_2^2-v_1^2)` (5)

v2: final speed of the box

v1: initial speed of the box = 0 m/s

You solve the equation (5) for v2:

`v_2 = \sqrt{(2W_T)/(M)}=\sqrt{(2(120.8J))/(36.0kg)}=2.58(m)/(s)`

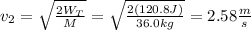
The final speed of the box is 2.58m/s