Answer:
The fourth mass should be located at (-1.506 m, -1.917 m).
Step-by-step explanation:
Given that each mass can be treated as puntual objects, the location of center of gravity can be determined by using weighted averages. That is:

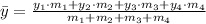
Where:
 ,
,
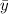 - Horizontal and vertical component of the location of the center of gravity, measured in meters.
- Horizontal and vertical component of the location of the center of gravity, measured in meters.
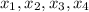 - Horizontal components of the location of first, second, third and fourth masses, measured in meters.
- Horizontal components of the location of first, second, third and fourth masses, measured in meters.
 - Vertical components of the location of first, second, third and fourth masses, measured in meters.
- Vertical components of the location of first, second, third and fourth masses, measured in meters.
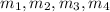 - Masses of first, second, third and fourth masses, measured in kilograms.
- Masses of first, second, third and fourth masses, measured in kilograms.
If
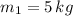 ,
,
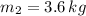 ,
,
 ,
,
 ,
,
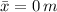 ,
,
 ,
,
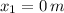 ,
,
 ,
,
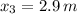 ,
,
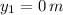 ,
,
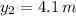 and
and
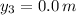 , then:
, then:

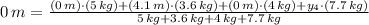
Both expression are simplified hereafter:
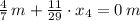
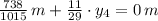
The solution of this system of equation is
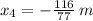 (
(
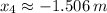 ) and
) and
 (
(
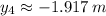 ).
).
The fourth mass should be located at (-1.506 m, -1.917 m).