Question

Refer to the Scheer Industries example in Section 8.2. Use 6.83 days as a planning value for the population standard deviation.

a. Assuming 95% confidence, what sample size would be required to obtain a margin of error of 1 days (round up to the next whole number)?
b. Assuming 90% confidence, what sample size would be required to obtain a margin of error of 2.5 days (round up to the next whole number)?

Answer 1

a)Sample size would be required to obtain a margin of error of 1 days is

n = 179

b) sample size would be required to obtain a margin of error of 2.5 days is n = 20

Explanation:

step(i):-

Given Population standard deviation = 6.83 days

a) Given margin of error = 1 day

The margin of error is determined by

`M.E = (Z_(\alpha ) S.D )/(√(n) )`

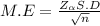
Step(ii):-

Given 95 % of confidence level

Now the critical value Z₀.₀₅ = 1.96

`1 = (1.96 X 6.83 )/(√(n) )`

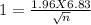
√n = 13.38

Squaring on both sides, we get

n = 179.206

b)

step(i):-

a) Given margin of error = 2.5 day

The margin of error is determined by

`M.E = (Z_(\alpha ) S.D )/(√(n) )`

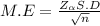
Step(ii):-

Given 90 % of confidence level

Now the critical value Z₀.₁₀ = 1.645

`2.5= (1.645 X 6.83 )/(√(n) )`

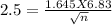
Cross multiplication , we get

`√(n) = (1.645 X 6.83 )/(2.5 )`

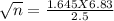
√n = 4.494

Squaring on both sides, we get

n = 20.19

Final answer:-

a)Sample size would be required to obtain a margin of error of 1 days is

n = 179

b) sample size would be required to obtain a margin of error of 2.5 days is n = 20