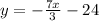Question

A direct variation function contains the points (-9, -3) and (-12,4). Which equation represents the function?

Answer 1

`y = -(7x)/(3) - 24`

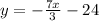
Explanation:

We can model this function using the equation of a line:

`y = ax + b`

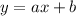
Where a is the slope of the line and b is the y-intercept.

To find the values of a and b, we can use the two points given:

(-9, -3):

`-3 = a * (-9) + b`

`-9a + b = -3`

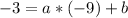
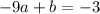
(-12, 4):

`4 = a * (-12) + b`

`-12a + b = 4`

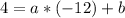
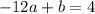
If we subtract the second equation from the first one, we have:

`-12a + b - (-9a + b) = 4 - (-3)`

`-12a + 9a = 4 + 3`

`-3a = 7`

`a = -7/3`

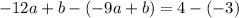
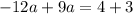
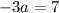
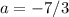
Then, finding the value of b, we have:

`-12a + b = 4`

`28 + b = 4`

`b = -24`

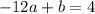
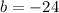
So the equation is:

`y = -(7x)/(3) - 24`