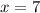Answer:
Part A:


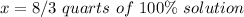

Part B:
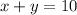
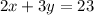
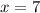 and
and
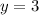
Explanation:
Part A:
The inicial concentration of the lemonade is 50%, and the volume is 4 quarts, and we will add x quarts of a lemonade with a concentration of 100%, so the total volume will be y, and the concentration will be 0.7, so we have that:


Using the value of y from the first equation in the second one, we have:
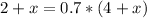

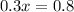
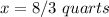
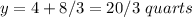
Part B:
If he shoots a total of ten targets, we can write the equation:
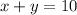
Each stationary target is 2 points, and each moving target is 3 points, so if the total points is 23, we have:
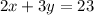
If we subtract the second equation by two times the first one, we have:


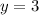
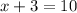 ⇒
⇒