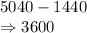Question

In how many ways can 8 people be seated around a circular table if 2 people aren't aloud to sit next to each other?

Answer 1

3600

Explanation:

Given that there are 8 people to be seated around a circular table.

As per formula:

Number of ways that they n people can sit around a circular table =
`(n-1)!`

We know that 2 people of out of these 8 are not allowed to sit together.

If we subtract the number of ways of these 2 people sitting together from the total number of ways of sitting of 8 people, we will get the number of ways that these 2 people do not sit together.

Number of ways of 2 people not sitting together = Total number of ways of 8 people sitting - Number of ways these 2 people sitting together.

Using formula:

Total number of ways =
`(8-1 )! = 7! = 5040`

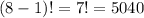
Let these two people always sit together, so these 2 can be thought as one pair.

So, 6 people and 1 pair,

Total number of ways the 2 people sitting together =
`(7-1)! * 2 = 6! * 2 = 720 * 2 =1440`

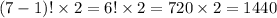
Total number of ways that the two do not sit together =

`5040 - 1440\\\Rightarrow 3600`