Question

Match each statement with its corresponding value for the system below: y = (2) ^x and y = 3x

1. The y-intercept of the linear function. 0 2.The y-intercept of the exponential function. 1 3.The number of points of intersection. 2 4.The quadrant of the solution(s). 1/2

Answer 1

1. The y-intercept of the linear function. 0

2.The y-intercept of the exponential function. 1

3.The number of points of intersection. 2

4.The quadrant of the solution(s). 1

Explanation:

The given functions are

Exponential function :
`y=2^x`

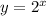
Linear function :
`y=3x`

Substitute x=0 in the above functions to find the y-intercepts.

`y=2^(0)=1`

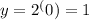
The y-intercept of the exponential function is 1.

`y=3(0)=0`

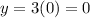
The y-intercept of the linear function is 0.

Plot the graph of both functions as shown below.

From the graph it is clear that both functions intersect each other at 2 points. So, the number of points of intersection is 2.

From the graph it is clear that both intersection points lie in first quadrant. So, the quadrant of the solution(s) is 1.