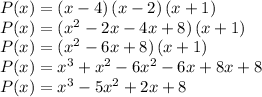Answer:
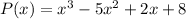
Explanation:
If the polynomial has the following zeros: x= 4, x=2, and x=-1, then it must have the following factors which guarantee the polynomial will render zero at the given points:
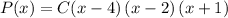
where C is any multiplicative constant. Since there is no other condition imposed on the polynomial, we can adopt a simple constant C = 1 to facilitate our final calculation of writing the polynomial in standard form: