Question

Determining the Input Value That Produces the Same Output

Value for Two Functions

If f(x) = -3x + 4 and g(0) = 2, solve for the value of x

for which f) = 9(26) is true

2=0.5

3

2

1

-2

2

3

Intro

Done

Answer 1

Corrected Question

If f(x) = -3x+4 and g(x) = 2, solve for the value of x for which f(x) = g(x) is true.

Answer:

`x=(2)/(3)`

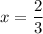
Explanation:

Given the functions:

• f(x) = -3x+4
• g(x) = 2

When f(x)=g(x), we have:

-3x+4=2

Collect like terms by subtracting 4 from both sides

-3x+4-4=2-4

-3x=-2

Divide both sides by -3 to solve for x.

`(-3x)/(-3)=(-2)/(-3)\\ x=(2)/(3)\\$Therefore, $f((2)/(3))=g((2)/(3))`

We conclude therefore that at
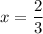`x=(2)/(3)` , the values of f(x) and g(x) are equal.