Question

Sara has 20 sweets. She has 12 liquorice sweets, 5 mint sweets and 3 humbugs. Sarah is going to take, at random, two sweets Work out the probability that the two sweets will not be the same type of sweet. Any help will be great! Thanks.

Answer 1

111 / 190

Explanation:

Let us first compute the probability of picking 2 of each sweet. Take liquorice as the first example. There are 12 / 20 liquorice now, but after picking 1 there will be 11 / 19 left. Thus the probability of getting two liquorice is demonstrated below;

`12 / 20 * 11 / 19 = (33)/(95),\\Probability of Drawing 2 Liquorice = (33)/(95)`

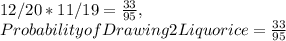
Apply this same concept to each of the other sweets;

`5 / 20 * 4 / 19 = (1)/(19),\\Probability of Drawing 2 Mint Sweets = 1 / 19\\\\3 / 20 * 2 / 19 = (3)/(190),\\Probability of Drawing 2 Humbugs = 3 / 190`

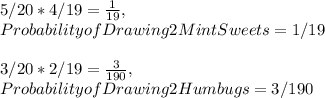
Now add these probabilities together to work out the probability of drawing 2 of the same sweets, and subtract this from 1 to get the probability of not drawing 2 of the same sweets;

`33 / 95 + 1 / 19 + 3 / 190 = (79)/(190),\\1 - (79)/(190) = (111)/(190)\\\\`

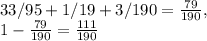
The probability that the two sweets will not be the same type of sweet =

111 / 190