Answer:
The probability that the average number of customers in the sample is less than 500
P(x≤500) = 0.1038
Explanation:
Step(i):-
Given average of customers per day 'μ' = 480
Standard deviation of customers 'σ' = 110
Given sample size 'n' = 48
Let x = 500
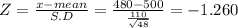
Step(ii):-
The probability that the average number of customers in the sample is less than 500
P(x≤500) = P(z≤-1.26)
= 0.5 - A(1.26)
= 0.5 -0.3962
= 0.1038
Conclusion:-
The probability that the average number of customers in the sample is less than 500 = 0.1038