Question

The following two-way table describes student's

after school activities. Find the probability that a
randomly selected student is in sports, given that
it's a senior.
Grade
Sports
Music/Drama
Work
Sophomore
20
7
3
Junior
20
13
2
25
5
Senior
5
P(Sports | Senior) = [?]
Round to the nearest hundredth.
Enter

Answer 1

0.71

Explanation:

P ( Sports | Senior ) =
`(P ( Sports|Senior ))/(P ( Total Senior))`

`(25)/(100) =25`

`(35)/(100) =35`

`(25)/(35) =0.714285=` 0.71

Answer 2

`P(Sports|Senior)= 0.71`

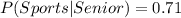
Explanation:

Hello!

You have a two-way table with the information describing students after school activities regarding the grade the student is in.

You have to calculate the probability that a randomly selected student is ins sports given that he is a senior.

This is a conditional probability and you can symbolize it as:

P(Sports|Senior)

Using the definition of the conditional probability we know that:

`P(Sports|Senior)= (P(Sports n Senior))/(P(senior))`

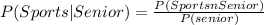
The probability of the intersection of both events "Sports" and "Seniors" can be calculated as the number of students that are in senior years and take sports by the total of students in the sample

P(Sports ∩ Senior)=
`(25)/(100)= 0.25`

The probability of the student being a senior is a marginal probability, you can calculate is as the number of observed students that are in senior year by the total number of students:

P(senior)=
`(35)/(100) = 0.35`

Now you can calculate the asked probability

`P(Sports|Senior)= (P(Sports n Senior))/(P(senior))= (0.25)/(0.35) = 0.71`

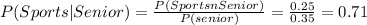
I hope this helps!