Question

A bicycle rider has a speed of 20.0 m/s at a height of 60 m above sea level when he begins coasting down hill. Sea level is the zero level for measuring gravitational potential energy. Ignoring friction and air resistance, what is the rider's speed when he coasts to a height of 18 m above sea level?

Answer 1

The rider's speed will be approximately 35 m/s

Step-by-step explanation:

Initially the rider has kinetic and potential energy, and after going down the hill, some of the potencial energy turns into kinetic energy. So using the conservation of energy, we have that:

`kinetic_1 + potencial_1 = kinetic_2 + potencial_2`

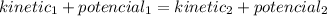
The kinetic and potencial energy are given by:

`kinetic = mass * speed^2 / 2`

`potencial = mass * gravity * height`

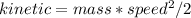
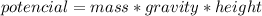
So we have that:

`m*v^2/2 + mgh = m*v'^2/2 + mgh'`

`20^2/2 + 9.81*60 = v'^2/2 + 9.81*18`

`v'^2/2 + 176.58 = 788.6`

`v'^2/2 = 612.02`

`v'^2 = 1224.04`

`v' = 34.99\ m/s`

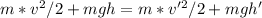
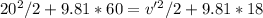
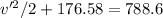
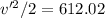
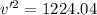
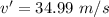
So the rider's speed will be approximately 35 m/s