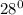Answer:
i ≅
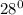
Step-by-step explanation:
Let the angle of incidence be represented by i, angle of emergence be represented by e, and angle of refraction by r.
Snell's law states that;
n =
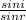 ................ 1
................ 1
where n is the refractive index of the prism.
Given that emergence =
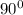
But from a ray diagram for the given question, we have;
 + (
+ (
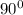 - r) + (
- r) + (
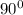 -
-
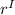 ) =
) =
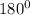 (sum of angles in a triangle) .................. 2
(sum of angles in a triangle) .................. 2
(
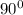 - r ) + (
- r ) + (
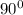 -
-
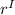 ) =
) =
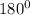 -
-

180° - (r +
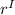 ) =
) =
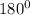 -
-

r +
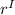 =
=

⇒ r =
 -
-
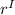 ........................ 3
........................ 3
The refractive index of the equilateral prism = 1.5.
Applying Snell's law to the refracting surface,
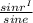 =
=
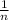
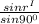 =
=
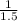
⇒
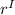 =
=
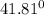
From equation 3,
r =
 -
-
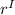
r =
 -
-
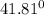
r =
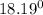
So that ;
n =
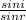
1.5 =
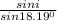
sin i = 0.4683
i =
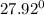 ≅
≅