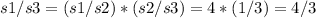Answer:
4/3
Explanation:
If the ratio between the volumes of the first and the second cube is 64, the ratio between the sides is the cubic root of the ratio between the volumes, so:
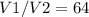
![s1 / s2 = \sqrt[3]{64} = 4](https://img.qammunity.org/2021/formulas/mathematics/high-school/h0gx8gxaj7pc6rqxrvr4v1o1ggv61fatl4.png)
Doing the same for the second and third cubes, we have:

![s2/ s3 = \sqrt[3]{1/27} = 1/3](https://img.qammunity.org/2021/formulas/mathematics/high-school/wwtpxy9qe0qs2p0dqji6lr6ebtg3bmbggb.png)
So the ratio of the first cube side and the third cube side is: