Question

A(n) 712 kg elevator starts from rest. It moves upward for 3.13 s with a constant acceleration until it reaches its cruising speed of 1.93 m/s. The acceleration of gravity is 9.8 m/s 2 . Find the average power delivered by the elevator motor during this period. Answer in units of kW.

Answer 1

P = 7.61kW

Step-by-step explanation:

In order to calculate the power delivered by the elevator motor, you take into account the work done by the elevator against the gravitational force.

The work done by the elevator is given by:

`W_g=(F-Mg)h=Mah` (1)

F: force of the motor

M: mass of the elevator = 712 kg

g: gravitational force = 9.8 m/s^2

h: vertical distance traveled by the elevator

a: acceleration of the elevator

You calculate the acceleration a by using the following formula:

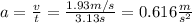`a=(v)/(t)=(1.93m/s)/(3.13s)=0.616(m)/(s^2)` (2)

With this values you can calculate F from (1)

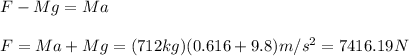`F-Mg=Ma\\\\F=Ma+Mg=(712kg)(0.616+9.8)m/s^2=7416.19N` (3)

Furthermore, you have that the work is equal to the change in the kinetic energy:

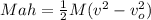`Mah=(1)/(2)M(v^2-v_o^2)` (2)

v: final speed of the elevator = 1.93 m/s

vo: initial velocity = 0 m/s

From the equation (2) you can calculate the vertical distance h:

`h=(v^2)/(2a)=((1.93m/s)^2)/(2(0.616m/s^2))=3.02m`

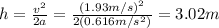
Then, the work done by the elevator is

`W_e=Fh=(7416.19N)(3.02m)=22422.53J`

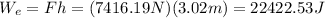
The quotient of the work We and time (3.13 s) is the power delivered by the motor:

`P_e=(W_e)/(t)=(22422.53J)/(3.13s)=7613.74W\approx7.61kW`

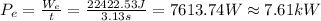
The power delivered by the elevator is 7.61kW