Question

A block of mass M is suspended from a ceiling by a spring with spring stiffness constant k. A penny of mass m is placed on top of the block. What is the maximum amplitude of oscillations that will allow the penny to just stay on top of the block

Answer 1

Step-by-step explanation:

Given that:

Mass of block M

Mass of penny m

spring stiffness constant k

The frequency of oscillation of the block
`f=(1)/(2\pi)\sqrt{(k)/(m) }`

The angular velocity is
`\omega =2\pi f`

`=√(k/m)`

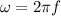
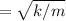
when the penny is resting on the block

The acceleration of the penny = acceleration of the block

If R is the reaction of the block on the penny

`R-mg=a_(max)m\\\\=-\omega^2A_(max)m\\\\R=mg-\omega^2A_(max)m`

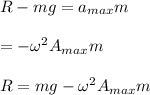
The penny will leave the block if R = 0

`mg=\omega^2A_(max)m\\\\g=\omega^2A_(max)\\\\A_(max)=(g)/(\omega^2) \\\\=(g)/((k/M)) \\\\A_(max)=gM/k`

Therefore the amplitude
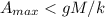`A_(max)<gM/k` for the penny to remain on the block