Answer:
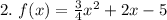
Explanation:
Given
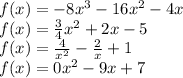
Required
Which of the above is a quadratic function
A quadratic function has the following form;
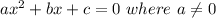
So, to get a quadratic function from the list of given options, we simply perform a comparative test of each function with the form of a quadratic function
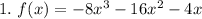
This is not a quadratic function because it follows the form
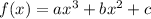 and this is different from
and this is different from
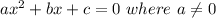
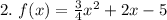
This function has an exact match with
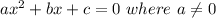
By comparison;
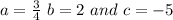
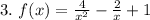
This is not a quadratic function because it follows the form
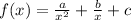 and this is different from
and this is different from
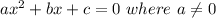
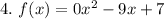
This is not a quadratic function because it follows the form
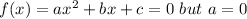
Unlike the quadratic function where
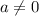
So, from the list of given options, only
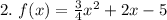 satisfies the given condition
satisfies the given condition